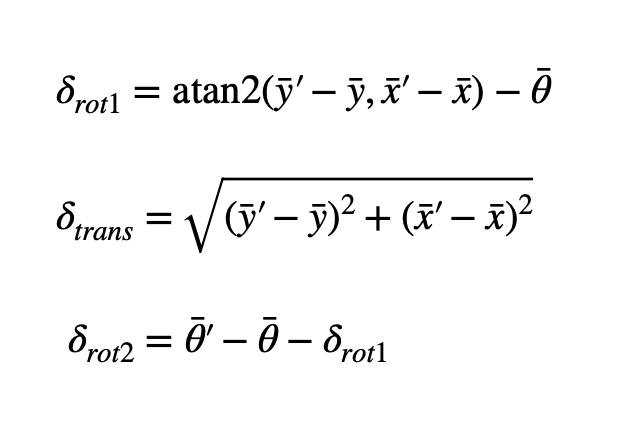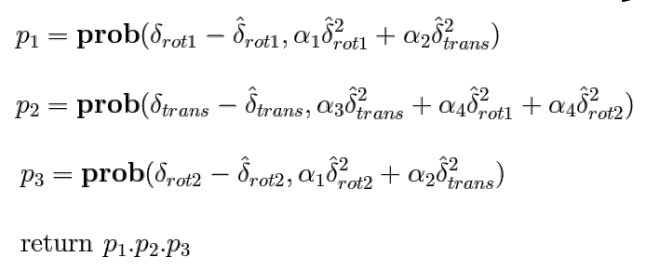Implementation
To implement the Baye's filter in the simulation environment, we had to complete the 5 main functions for the
prediction and update steps.
Function 1: compute_control()
The first function to implement was compute_control. This function takes in a current position and a previous
position and calculates the 3 main odometry control values: rotation_1, translation and rotation_2. I used the
equations given in the lecture slides to compute these values from the given positions. I also had to make sure to
normalize the two rotations so that they are within the -180 to 180 deg range.
Function 2: odom_motion_model()
The second function to implement was odom_motion_model. This function takes in a current position, a previous
position and a control input u. The output of this function is the probability of each parameter, calculated as
a Gaussian distributions with mean from u, which is essentially p(x'|x, u). This is just the probability of a
state given a prior state and action. The function first extracts each of the 3 model
parameters by calling
compute_control(). Then we use loc.gaussian() to calculate each individual parameter probability. The output is
just these 3 probabilities multiplied.
Function 3: prediction_step()
The third function to implement was prediction_step(). This function takes in two parameters, the current and
previous odometry parameters. It performs the predict step of the Baye's filter.
It first calculates the control variable u using computer_control() then initializes a new belief loc.bel_bar to
0. It loops over every possible prior cell (x,y,θ) with non-negligible belief, defined by
a probability threshold (as said in the lab handout I chose a threshold of 0.0001), and every possible new
cell (x',y',θ'). It then converts both grid indices into real poses via the mapper, and uses the odometry motion
model to compute the likelihood of moving from (x,y,θ) to (x',y',θ') given u.
Each of these transition probabilities is weighted by the old belief at (x,y,θ) and
accumulated into
bel_bar[x',y',θ']. Finally, I normalized bel_bar so that the total probability sums to one.
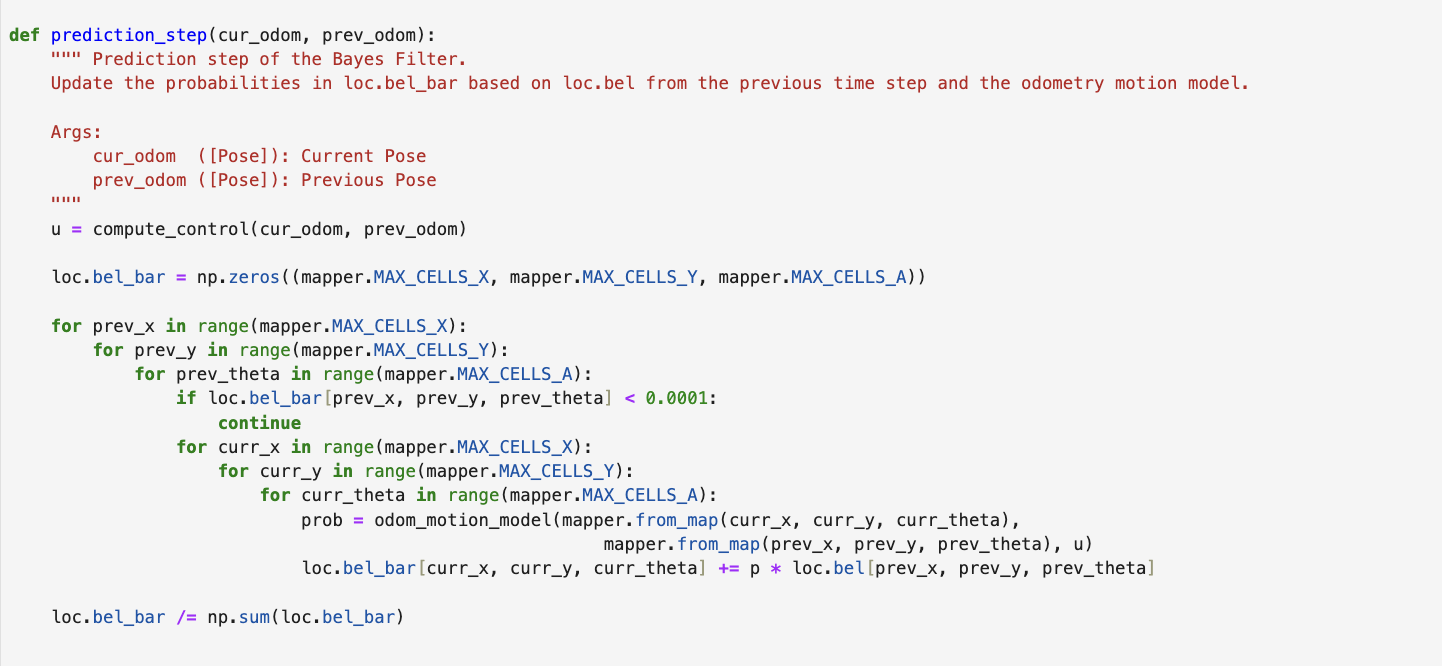
This step of the Baye's filter can be highly computationally inefficient since it loops through all the possible
cells. Therefore, to reduce computation we set a threshold and only loop through all prior cells with a certain
threshold of belief.
Function 4: sensor_model()
The fourth function to implement was sensor_model(). This function takes in one parameter, the true observations
of the robot in the map for a particular pose. It then outputs p(z|x), which is the probability of the given
oberservation given a current state. I used loc.gaussian() to calculate each probability using the observation
data as the mean.
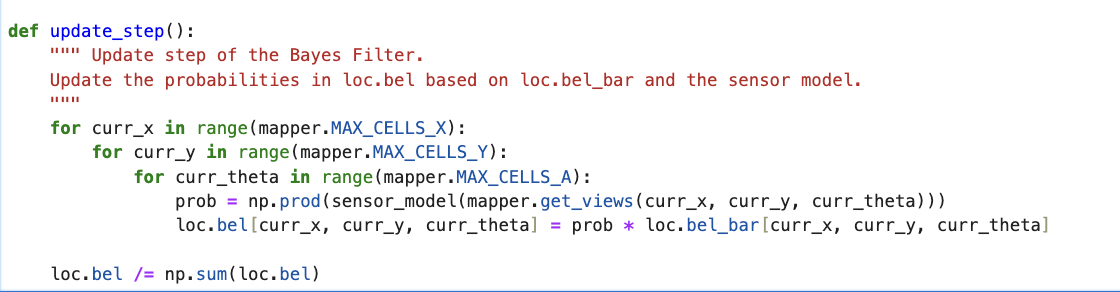
Function 5: update_step()
The last function is the update_step() of the Baye's filter. This function loops over the grid for the
current states and uses the sensor_model() function to retrieve the probability array. This probability value is
then used to update loc.bel. Finally, I normalized bel so that the total probability sums to one.